矩阵分析法：通过两个维度矩阵发现问题

更新: 7/18/2025 字数: 0 字 时长: 0 分钟

矩阵分析法本质上是一种用两个指标来找判断标准的方法，它的操作非常简单。

第一步：找到两个评价指标，每个指标取平均值作为判断标准。
第二步：两个指标交叉，得出4个象限，将样本根据评价指标大小，分散到4个象限里。
第三步：根据两个指标的含义，给出4个象限的含义解读，对每个样本进行分类。

只要两个指标的相关性高，当两个指标交叉的时候，数据就会被分散在4个象限里，这样能清楚地找到业务含义。 还以100家门店为例，如果补上当月的成本数据，则可以构造收入/成本矩阵。

第一步：先对收入/成本两个指标单独求平均值，区分出高收入/低收入、高成本/低成本。
第二步：两个指标交叉，给门店标上状态(高收入+低成本、高收入+高成本、低收入+低成本、低收入+高成本，共4类)。
第三步: 统计4类门店的数量、收入、支出数据，再计算利润(利润=收入-支出)，可得到的数据如表所示(数据的差异是四舍五入后造成的)。

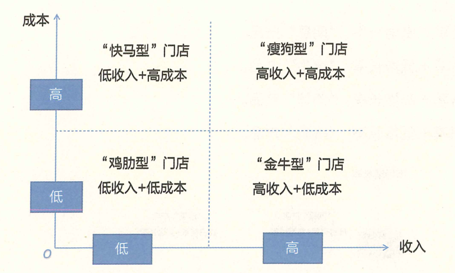
进一步，还可以根据分类给这些门店起一些好听的、容易记的名字，比如。

• 高收入、低成本：“金牛型”门店。
• 高收入、高成本：“瘦狗型”门店。
• 低收入、低成本：“鸡肋型”门店。
• 低收入、高成本：“快马型”门店。

这样能让矩阵分析的结果更容易展示，从而更方便应用，如图所示

如果把100家门店的数据代入，则可以通过散点图进行观察，如图所示

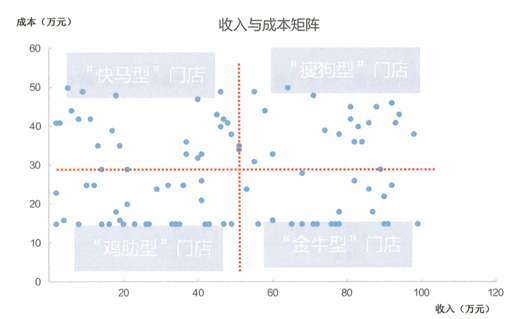
从上图中可以直观地看出来，哪些门店是“金牛型”门店，哪些门店是“鸡肋型”门店，哪些门店是“快马型”门店，哪些门店是“瘦狗型”门店。这种清晰的分类，能很直观地引人思考。

• “快马型”门店是不是可以增加投入，做得更多一些?
• “瘦狗型”门店出了什么问题，要怎么改善?

这就达到了矩阵分析法的目的: 在两个评价指标不相关的情况下，得出判断结论。

通过这个案例可以看出，构造矩阵能很轻松地发现问题。对构造矩阵来说，如何选择组成矩阵的两个维度非常重要。一些维度选得好的经典矩阵，比如“波士顿矩阵”，已经成为咨询公司的常用方法。如图所示，通过调研自身产品的市场占有率与市场增长率，就能区分出产品的种类了。

• 高占有率+高增长率：“明星”产品。
• 高占有率+低增长率：“金牛”产品。
• 低占有率+高增长率：“问题”产品。
• 低占有率+低增长率：“瘦狗”产品。

当有两个指标参与评价时，如果两个指标高度正相关，一个指标涨了，另一个指标也会涨,此时不需要做矩阵分析。只要对其中一个指标进行评价，另一个指标的结果就不会有大的差异。这种相关关系可以简单地用散点图来呈现，如图所示。

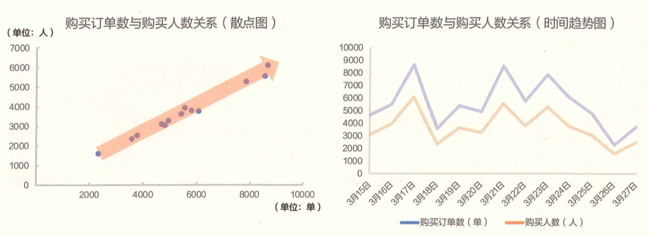
但是，有可能两个指标不是高度正相关，比如，投入和产出指标，可能存在下面的情况。

• 某间门店经营不善，收入锐减，但是成本不变(高投入、低产出);
• 某个新市场刚刚被发现，竞争少，投入一点就收入颇丰(低投入、高产出)

这时，不能简单地用某一个指标来评估利弊，而是要先分清有几种情况，我们可以用矩阵分析法。

但是要注意，过去的成功不代表未来的成功，不能仅仅靠矩阵分类来作为未来行动的依据。比如在上例中，所有高收入、低成本的门店，本身的整体收入并不高，很有可能是这些门店都是新开的门店,还处在上升阶段：或者开店的位置比较好,比如新开盘的小区，附近竞争对手少很有可能之后这种优势就会消失。如果仅仅看到这张图就下令大力发展这些“快马型”门店,则很有可能遭到失败。

所以，矩阵分类法的作用是识别出异常值，发现潜在问题，而非直接得出结论。矩阵分析法的短板在于仅关注一个时间点的表现，不能纵观前后发展趋势。如果考虑成本/收入指标的前后趋势，就需要用到“盈亏平衡分析法”。